数学和美是有关系的,因此建筑师通常会将数学、科学和艺术结合起来,创造出有吸引力的功能性结构。这方面的一个典型例子就是利用黄金分割的原理来达到和谐比例。黄金分割是数学原理的一个公式,它被认为能产生令人满意的比例。黄金分割的例子在自然界中广泛存在,包括人体。多年来,许多著名的艺术家和建筑师将黄金分割应用到他们的作品中,如达·芬奇和米开朗基罗,用黄金分割来定义他们作品的尺寸和比例。
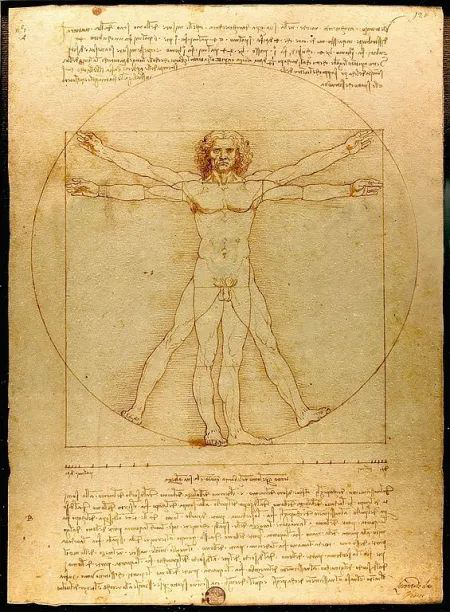
帕台农神庙就受到了数学原理的影响,它是由建筑师伊克蒂诺斯和卡尔利克拉特斯设计的。神庙有两个房间来存放雅典娜女神的黄金和象牙雕像以及她的财宝。游客从外面可以观看雕像和神庙。它精致的外观因其比例和谐而闻名,并影响了几代设计师。

数学是建筑的一个重要工具,建筑随着数学的变化而变化。这种关系最明显的例子是2D和3D计算机辅助设计程序,它们是现代建筑实践的基础,几乎完全基于数学原理。
Minifie Nixon设计的维多利亚学院艺术中心表达了一个既漂亮又有用的数学概念,叫做冯洛诺伊图(Voronoi diagram),也就是泰森多边形。每个冯洛诺伊图由一组点定义。想象一下,一个三岁的孩子用钢笔在一张纸上画了许多点(离散点)。对于每一个点,你可以找到一组白色的点比其他钢笔画的点更接近它,我们称这组点为“细胞”。如果画出所有“细胞”的边界,形成多个多边形,就会得到一个冯洛诺伊图。假设只有有限的钢笔点,那这些图形都是由直线定义的。

扎哈·哈迪德在转向建筑之前学习数学,因此她追求支离破碎的几何图形和多重视角,对于建筑和数学逻辑之间的逻辑关系了解的十分清晰。她的作品被描述为新未来主义,以其高度复杂和富有挑战性的设计而闻名,无论是字面上还是隐喻上,这些设计都突破了界限。

创造性建筑和现代建筑技术的结合创造了令人印象深刻的建筑形体。其中离散微分几何也在这个领域发挥了作用。奥地利科学基金会FWF进行的一个数学项目的结果显示了数学基础研究是如何帮助建筑师实现惊人的建筑概念的。

下图展馆设计的基本单元是谢尔宾斯基三角形(Sierpinski triangle),这是一个纯粹的分形形式,提供了结构的稳定性和技术的坚固性。主体结构框架采用竹桁架,在竹桁架上编织分形设计的竹网格。最后,丙烯酸玻璃材料被固定在格子上。利用谢尔宾斯基三角的基本单位,基本什么都不用就能获得结构稳定性。

从上面的例子中可以看出,数学原理的应用可以产生一些非常惊人的架构,建筑师的作品反而会更加具有引人注目的和谐度与平衡感。这也是为什么很早之前的古建筑也会用通过数学模型来体现出舒适的外观。接下来我们来看看在一些学术方案中,数学之美是如何被设计者巧妙的体现出来的~
一、 莫比乌斯桥
Hakes Associates设计的莫比乌斯桥是一座时尚而性感的人行桥,与行人对话,且不会干扰到周围的景色。莫比乌斯桥的设计是由Buro Happold合作开发的,是Hakes Associates风格的典型例子,灵感来自无尽的莫比乌斯环路。行人和自行车过河是一个动态的、连续的系结结构,它在物理和结构上独立于两个河岸,以避免可能破坏邻近建筑和遗址上的考古遗迹等。

桥梁的几何形状经过场地的约束和精心选择,产生了一个有效的结构解决方案。主跨度由受压的钢拱组成,桥面由直径较小的吊索悬挂。桥面部分作为横梁跨越剩余的距离,并在拱门和桥面之间有一个连接。建筑赋予了这座桥雕塑的特征,使它可以成为一个地标和数学艺术再生的象征。

二、 建筑中的线性系统
几个世纪以来,建筑师一直受到自然形态和几何图形的启发。他们的设计受到了结构、比例、颜色、图案和质地的影响。建筑师已经将这些影响融入到主要是经验的过程中。只是在过去的几十年里,人们才更好地理解了自然形式的许多潜在的逻辑、数学。20世纪60年代末,生物学家阿里斯蒂德·林登迈尔提出了一种字符串重写算法,这种算法可以极其轻松地模拟简化的植物及其生长过程。这个理论现在被称为线性系统(Linear system)。

模块化线性系统桁架
这个项目研究L-system是否能在建筑领域打开可能性,以及应用于建筑形式的生产方式和额外功能。上述的线性系统算法可以被扩展以促进建筑几何的产生。图形命令被用来控制三维空间的运动。通过将可变参数直接引入图形语言,可以获得更大的几何自由度。最后,该系统被扩展到环境交互,这样就可以根据当地条件执行不同的字符串。

参数线性系统

随机线性系统
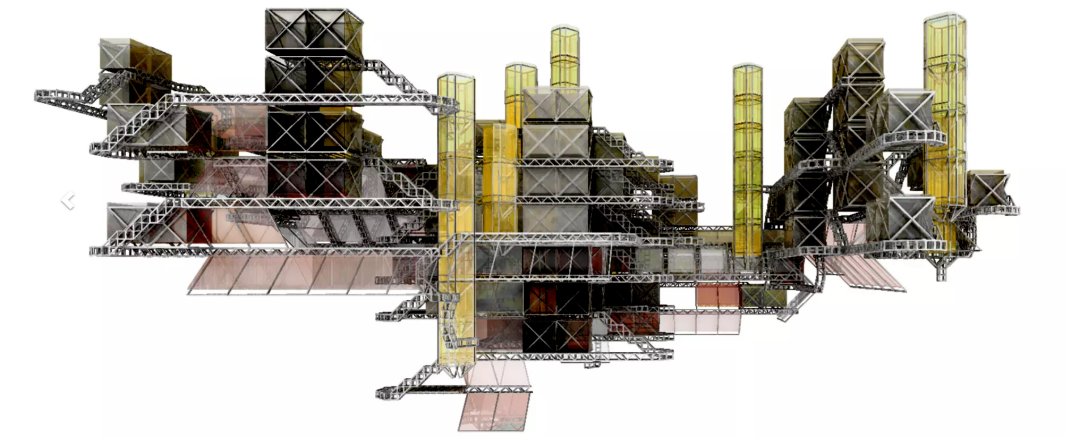
模块化线性系统
代替固定的替换规则,可以引入随机规则,使得字母被具有特定概率的第一个字符串替换,否则被另一个字符串替换。事实上,任何数量的替换场景都是可以想象的。由此产生的系统产生了由替换过程中的随机数引起的不规则分支结构。通过允许这些随机数在系统每次运行时也波动,可以产生设计的许多不同排列。
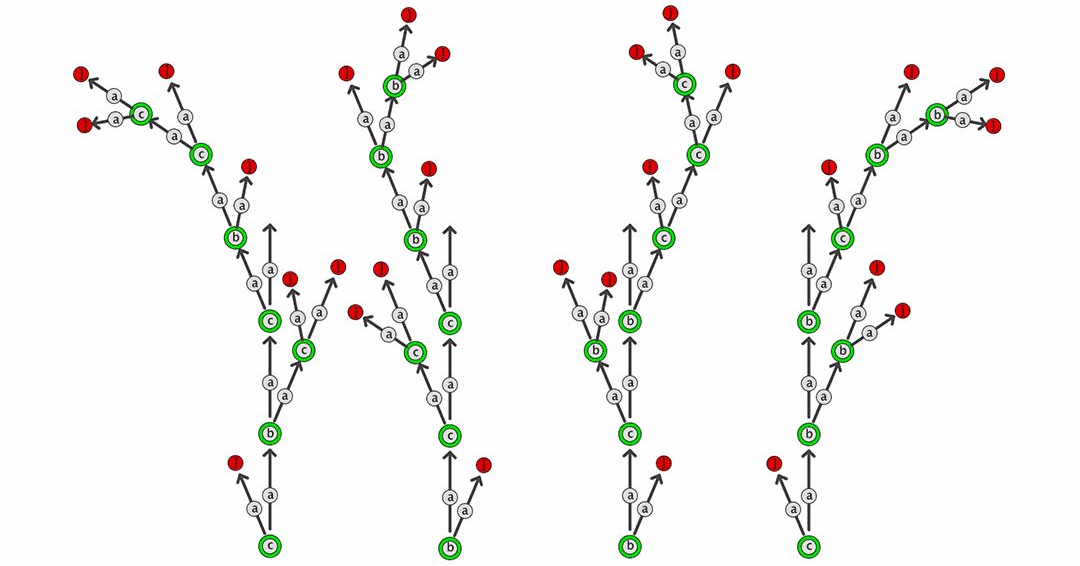
线性系统逻辑特别适合模块化系统的生产。由于不是字符串的每个字母都需要对应一个图形指令,所以可以引入一些字母,这些字母可以简单地被其他字母组所代替。例如,在一个系统中a意味着前进c意味着向右转,一个新的字母d可以定义为创建一个正方形:d=acacaca。并且线性系统逻辑不仅可以用来创建组件的空间组织,还可以用来区分和表达这些组件。通过在组件定义中引入参数,组件变得灵活并适应当地条件。

线性系统可以是一个强大的设计工具。最少的输入可以产生空间上复杂的输出。字符串重写逻辑特别适合包含分支、递归和模块化的表单。通过扩展逻辑以包括独立的参数,人们不仅可以获得对产生形式的高度控制,还可以潜在地变得自适应。因此,形状的结构参数可以与空间位置、方位,甚至与已经生产的组件联系起来。
本文来源ImpactStudio ,作者Harley,如有侵权请联系删除,谢谢!

